
1.0 Innledning..............................................s. 1
2.0 Geometri i M-87 og Veiledende Årsplan...................s. 2
3.0 Læringsmodeller.........................................s. 3
3.1 Piagets læringsmodeller.........................s. 3
3.2 Van Hiele nivåer................................s. 4
4.0 Hvorfor vi vil benytte van Hiele........................s. 5
5.0 Tanker om nivå 1........................................s. 6
5.1 Innledning......................................s. 6
5.2 Presentasjon av geometriske figurer.............s. 9
5.3 Begrepsdanningen...............................s. 11
5.4 Eksempler og ikke-eksempler....................s. 13
6.0 Van Hieles 2 nivå......................................s. 15
6.1 Innledning til nivå 2..........................s. 15
7.0 Sluttord...............................................s. 18
8.0 Litteraturliste........................................s. 19
Denne oppgaven er derfor mer tanker vi har gjort oss omkring innføring av geometri enn det er et komplett opplegg. Vi presenterer forslag til fremgangsmåter med bakgrunn i undersøkelser, praksis og rådende teori på området. Det vi ønsker å påpeke, er tankene en må gjøre seg før en innfører nytt stoff.
Vi må videre presisere at oppgavene vi presenterer ikke har noen som helst tidsavgrensing. De fremgangsmåtene vi legger frem er ment å representere et stadium i læringen som som ofest går fra 1. - 2. klasse. Avslutningsvis kommer vi så vidt inn på hvordan en viderefører opplegget til et noe høyere nivå (3. - 4. klasse).
Mønsterplanen fremhever geometrien som et sentralt emne innenfor matematikken. Begreper som blir brukt for å beskrive geometriske figurer og former, er begrep som går igjen i dagliglivet. På den måten blir geometri et nyttig redskap for å beskrive omverdenen.
En annen viktig side ved geometrien er at den er godt egnet for eksperimentering og utforskning. Dette på grunn av den nære tilknytningen til tegning og skapende arbeid.
Dette lar seg blant annet gjennomføre ved å inspirere elevene til å bruke skisser og fri tegning for å beskrive geometriske objekter.
I innføringen av geometri ( 1.- 3.klasse ), fremsetter mønsterplanen følgende emner:
van Hieles nivåtenkning er en læringsmodell som blir stadig mer populær, særlig innen undervisningen i geometri. Denne modellen er en strikt ovenfra-og-ned modell. Før en kan gå videre på et nytt nivå må det foregående beherskes. Derimot spiller ikke elevens alder eller modenhet noen stor rolle for om han skal kunne gå fra et nivå til et annet. Dette avhenger mer av måten undervisningen legges opp på.
Nivåene er(Hedrén, side 29; Dickson, side 18):
Hvordan lærer barn geometri ? I mange lærebøker får barna sitt først møte med geometri gjennom en presentasjon av linjer, rektangler og sirkler som grupper av punkter som oppfyller visse krav.
Hva ligger bak en slik måte og starte opp geometriundervisningen på ? Ubevisst antar en kanskje at barn ikke er spesielt ulik voksne, at de har et velutviklet apparat for logisk tenkning. Men bl.a. Piaget har gjennom undersøkelser(Copeland(1972), side 23) påvist at barn ikke er i stand til å se at den minste biten et linjestykke kan deles opp i er et punkt. Helt opp i 11-års alderen vil de insistere på at den minste delen et linjestykke kan deles opp i er et annet linjestykke. Ikke før det når Piagets 4. stadium (11-12 års alderen) er barnet i stand til å forstå begrepet punkt.
Elevene vil så smått starte med geometri allerede i første klasse. Og de vil da befinne seg på Piagets 2. eller 3. stadium. Bare unntaksvis vil noen av dem ha stiftet bekjenntskap med et så abstrakt begrep som et punkt. Men alle vil å støtt på geometriske figurer; kjøkkenbordet hjemme, hjulene på sykkelen, kumlokk, i melkeboksen....
På dette grunnlaget finner vi det naturlig å benytte oss av van Hieles metoder, som ser ut til å gi en god tilnærming til emnet.
Begrepsinnhold - B.I - er tankene vi har om ting vi omgir oss med, det er den betydning vi som enkeltindivid tillegger våre erfaringer. B.I blir derfor i stor grad subjektivt.

Begrepsuttrykk - B.U - er språk som symboliserer tankene, meningene. B.U er språk i vid betydning: muntlig språk, tegn, kroppsspråk.......
Denne sammenhengen mellom B.I og B.U finner vi også hos semiologen Sausure. Han understreker at de er avhengige av hverandre og påvirker hverandre.
Når vi nå i det følgende skal beskrive et opplegg for å hjelpe elever til å utvikle kunnskaper om geometriske figurer som tilsvarer Van-Hieles første nivå, blir det naturlig å gripe fatt i språket som en viktig innledende faktor.
Et lite barns første handlinger, før språklig utvikling, er nesten utelukkende basert på "erfaringer" med gjenstander i rom(Dickson, side 12). Barnet bruker sanser som syn og følelse (ta på ) for å forstå og tolke omgivelser. Denne erfaringen tar det med seg videre i livet. Når så språkets finurligheter åpner for en ny måte å uttrykke meninger og tanker på, opplever barnet at det prøver å si ikke alltid tilfredsstiller de voksnes forventninger.
Her er vi inne på et tema som kan være med på å bremse mattelæringen; - språklig utilstrekkelighet. Vygotsky snakker om språk av 1.orden. Med det mener han uttrykk som står i direkte kontakt med begrepsinnholdet. Selv om barn ofte kan ha vanskeligheter med å sette ord på tanker, er ikke det samme som at de ikke har noe de ønsker å uttrykke. (Dickson(1974), side 7)
Dette er det viktig at vi som mattelærere er oppmerksomme på når vi skal innføre noe nytt som geometriske figurer. Vi må finne en naturlig kobling mellom elevenes tidligere erfaring og det vi ønsker å formidle. Vi må la dem få utvikle et naturlig 1.ordens språk som setter dem istand til å uttrykke sine tanker om stoffet med ord både lærer og elev har dannet seg begrepsinnhold rundt. Når eleven sier: " dette er et rektangel", må vi ha sørget for å stimulere elevens erfaringer rundt det begrepet på en måte som gjør oss sikre på at hans indre bilde av et rektangel korresponderer med vårt, som forhåpentligvis er et matematisk korrekt bilde.
Vi mener derfor den beste innledningen til dette emnet blir som følger:
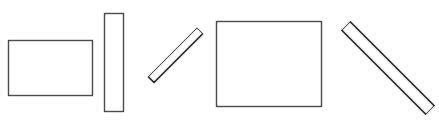
Samtale: Hva er dette? Hvordan ser de ut ? (lange,smale,korte). Vi ønsker at elevene med egne ord skal komme frem til figurenes "særegenheter". Finnes det likhetstrekk? Vi håper å få frem ord som; avlang, to korte, to lange.. Begrepet rektangel presenteres.
Samtale: Hvordan føles et rektangel?
Hvordan geometriske figurer presenteres av læreren på tavlen og i læreboken er av stor betydning for elevenes begrepsutvikling. Dersom læreren ikke hele tiden tenker over hvordan tavleundervisningen oppfattes av elevene kan han fort skape meget store problemer for elevenes begrepsutvikling. Vår erfaring er at geometriske figurer presenteres på tavlen på følgende måte:

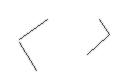
Dersom dette er den eneste måten elevene får møte disse figurene, kan dette føre til at når elevene presenteres for ikke-standard figurer så som dette,
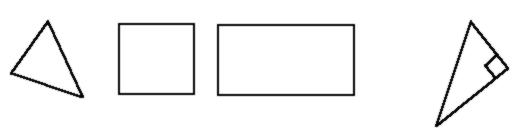
vil noen av dem, som uten særlige vansker identifiserer de geometriske figurene i fig. 1, ikke greie å identifisere korrekt de samme figurene i fig. 2.
Vi opplevde dette i praksis. På tavlen presenterte vi gjennomgående figurene som i fig. 1. Den siste mattetimen avholdt vi en liten prøve for å hjelpe oss å danne oss et bilde av hva vi hadde greid å lære klassen. Oppgave 2 var som følger: Sett rett navn på figurene:

Av figuren over ser vi at mens 80% av elevene identifiserte kvadratet korrekt i c), mens bare 40% gjenkjente figur f) som et kvadrat.
En annen ting vi observerte hos en av elevene(som identifiserte c) som en firkant) var at denne eleven identifiserte f) som en 'opp-ned firkant'. For denne eleven betyr en forandring i posisjon en forandring i egenskaper. Dette er et klart eksempel på at eleven ikke har fått mulighet til å internalisere begrepet kvadrat(eller for den saks skyld begrepet firkant). (Jmf. Greenes, sitert i Dickson, side 29).
Alle figurene innen en kategori må være av samme størrelse, men farge kan varieres.
Læreren blander disse og legger dem hulter til bulter på pulten og eleven sorterer brikkene i fire ulike hauger.
Varianter:
5.3.6a Tegn ikke figurene på tavlen.
5.3.6b Bruk så store figurer at eleven ikke kan føle
hele figuren på en gang.
5.3.6c Be elevene finne en figur med tre hjørner,
fem kanter, som er runde, osv.
En antagelse som gjør seg gjeldende hos mange lærere er at når eleven blir vist en figur på tavlen og blir fortalt at 'dette er et kvadrat', vil eleven 'avfotografere' figuren og lagre den til senere bruk. Ifølge Piaget er dette en grov overforenkling (Copeland(1972), side 24). Et par dager etter at læreren tegnet kvadratet på tavlen vil eleven kunne hente frem bildet av tavlen med kvadratet på, men etter en uke eller to vil det være glemt. Det som skjer er at bildet av kvadratet kun lagres i kort-tidsminnet(KTM); fordi eleven ikke har fått arbeide med og bearbeide begrepet kvadrat er det ikke blitt overført til langtidsminnet(LTM). Eleven har ikke dannet seg et indre bilde av hva et kvadrats egenskaper er.
En hovedtese hos Piaget er at 'Kunnskap er knyttet til arbeid'(Solvang, side 83). Dette arbeidet skjer ifølge Piaget både auditivt(eleven lytter til det læreren sier) og visuelt(eleven ser det læreren skriver på tavlen). Men eleven må også, på grunnlag av sine egne taktile(fysiske) erfaringer med figuren, danne seg en indre representasjon av den. For å oppnå dette er det er viktig at eleven gis mulighet til å samle så mange og forskjellige erfaringer som mulig om de geometriske formene. Oppgavene 5.3.1 til 5.3.4 foran vil hjelpe til med å gi disse erfaringene.
Oppgavene 5.3.5 - 5.3.6 kan hjelpe oss å se om elevene virkelig har utviklet de begrepene vi ønsker.
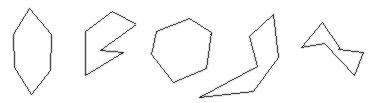
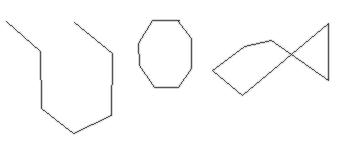
Kommentar:
Det er ikke alltid det er nok å vise ulike eksempler på hva f.eks. et rektangel er, ofte vil det hjelpe innlæringen av et begrep å vise eksempler på hva det ikke er. Men også disse ikke-eksemplene må velges med omhu.
Charles(Dickson, side 34) gir følgende retningslinjer for valg av eksempler og ikke-eksempler.
Når en elev har tilegnet seg kunnskaper om geometriske figurer som gjør ham istand til å analysere dem utfra egenskaper som parallellitet, flateberegning, omkrets, rette vinkler...., sier vi at eleven pr definisjon har oppnådd Van-Hieles andre nivå.
Opplegget vi har presentert til nå vil forhåpentligvis være tilstrekkelig for å skaffe elevene skikkelige basiskunnskaper, og forberede dem til videre "studier". Vi må få presisere angående nivå 1 opplegget, at det er et tidkrevende prosjekt, som ikke er ment å vare bare noen timer. Særlig samtalefasen innledningsvis bør vektlegges i særlig stor grad med konkretisering gjennom prosjekter med figurer og feltstudier.
Også et opplegg for nivå 2, vil bære i seg mange av de samme pedagogiske aspektene som det foregående. De samme "fellene" må unngås. Variasjon i oppstilling og presentasjon samt språkbruk må vektlegges. Vi vil i det følgende kort presentere hvordan en innledning til dette nivået kan se ut.
Hva vet vi om rektangler? (oppsummering). Rektangel er forhåpentligvis blitt et 1.ordens språk for eleven. Det bør ikke være behov for erstatningskoder for å knytte begrepsuttrykk med begrepsinnhold.
Oppgaver av typen hvor mange rektangler i ulike størrelser og posisjoner blir presentert, hvorpå eleven skal måle sidene, samt erfare at en vinkel er rett selv om den ikke står "beint" på arket.
Eks.:
Kerslake(Dickson, side 31) gjennomførte en undersøkelse blandt 10-åringer for å "kartlegge" deres kunnskaper om rette vinkler. Antall riktige svar er oppgitt i prosent:

Dette understreker viktigheten av å variere presentasjonen av nytt stoff.
Kerslake gjorde en lignende undersøkelse med parallellitet som emne. Resultatene ble som følger:
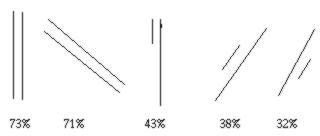
Lik lengde på linjene så ut til å ha blitt ett kriterium. Dette er momenter vi hele tiden bør ha i tankene når vi legger opp timer i innføringen av geometriske figurer.
Sirkler viser seg å være den av de geom. fig. som barn lettest lærer å gjenkjenne og konstruere (Noelting, sitert i Dickson, side 20). Men når en presenterer diameter og radius for elevene, er det lett å være for rask, slik at noen danner seg misoppfatninger rundt disse begrepene. Det erfarte vi i praksisen. Vi presenterte stoffet på følgende måte:
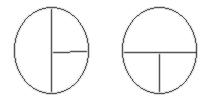
Resultatet ble at enkelte, faktisk ganske mange, fikk den oppfatningen at diameter kun eksisterte vertikalt og horisontalt. Hvis diameteren kom på skrå var det f.eks. en elev som ville kalle det en diagonal. Dette passer godt med undersøkelser gjort av Zykova(Dickson, side 36) med russiske 12.åringer. De hadde blitt presentert begrepene med "standardoppsett". De mente derfor at det fantes bare to diametrer i en sirkel.
Hvordan kan dette unngås? Elevene bør i mye større grad selv komme frem til hva diameter og radius er. Dette kan på en enkel måte gjøres gjennom konstruering.
Dette er eksempler på hvordan en ved hjelp av enkle midler og variasjoner, på en grei måte kan presentere nye begrep på en induktiv måte.
Analyse av geometriske figurer er et veldig omfattende emne. Vi har nå gitt noen tips om ting en bør være oppmerksom på. Overfører en dette til det videre arbeid med stoffet vil kanskje det gå lettere. Vårt poeng er å unngå fellene med standardoppsett. Vær kreativ og varier presentasjonen av et hvert nytt emne. Hvordan du fremstiller begrep, samt hvordan du ordlegger deg er av avgjørende betydning for læringsprosessen.
Dette er kun ment som en liten innledning på det omfattende stoffet som nivå 2 omfatter. Vi håper det kan være en spore for videre arbeid.
Gjennom arbeidet med denne oppgaven er vi blitt oppmerksomme på hvor viktig det er å ikke bli for standardisert i veiledningen. Det finnes utallige feller en kan gå i, som lett unngås med enkle middel. Vi håper vi med dette kan hjelpe og inspirere andre som på en eller annen måte arbeider med innføring av geometri.